I’ve been trying to learn Rust lately, the hot new
systems programming language. One of the projects I wanted to tackle with the
speed of Rust was generating 3D polyhedron shapes. Specifically, I wanted to
implement something like the Three.js
IcosahedronGeometry
in Rust. If you try to generate
icosahedrons in Three.js over any
detail level over 5 the whole browser will slow to a crawl. I think we can do
better in Rust!
Furthermore, I wanted to generate a hexsphere: a sphere composed of hexagon faces and 12 pentagon faces, otherwise known as a truncated icosahedron or the Goldberg polyhedron. The shape would be ideal for a game since (almost) every tile would have the same area and six sides to defend or attack from. There’s a few Javascript projects for generating hexspheres. Most of them generate the shape by starting with a subdivided icosahedron and then truncating the sides into hexagons. Though, there exist other methods for generating the hexsphere shape.
Play around with all of these shapes in your browser at: https://www.hallada.net/planet/.
So, how would we go about generating a hexsphere from scratch?
The Icosahedron Seed
To start our sculpture, we need our ball of clay. The most basic shape that we start with can be defined by its 20 triangle faces and 12 vertices: the regular icosahedron. If you’ve ever played Dungeons and Dragons, this is the 20-sided die.
To define this basic shape in Rust, we first need to define a few structs. The
most basic unit we need is a 3D vector which describes a single point in 3D
space with a X, Y, and Z float values. I could have defined this myself, but to
avoid having to implement a bunch of vector operations (like add, subtract,
multiply, etc.) I chose to import
Vector3 from the
cgmath crate.
The next struct we need is Triangle. This will define a face between three
vertices:
#[derive(Debug)]
pub struct Triangle {
pub a: usize,
pub b: usize,
pub c: usize,
}
impl Triangle {
fn new(a: usize, b: usize, c: usize) -> Triangle {
Triangle { a, b, c }
}
}
We use usize for the three points of the triangle because they are indices
into a Vec of Vector3s.
To keep these all together, I’ll define a Polyhedron struct:
#[derive(Debug)]
pub struct Polyhedron {
pub positions: Vec<Vector3>,
pub cells: Vec<Triangle>,
}
With this, we can define the regular icosahedron:
impl Polyhedron {
pub fn regular_isocahedron() -> Polyhedron {
let t = (1.0 + (5.0 as f32).sqrt()) / 2.0;
Polyhedron {
positions: vec![
Vector3::new(-1.0, t, 0.0),
Vector3::new(1.0, t, 0.0),
Vector3::new(-1.0, -t, 0.0),
Vector3::new(1.0, -t, 0.0),
Vector3::new(0.0, -1.0, t),
Vector3::new(0.0, 1.0, t),
Vector3::new(0.0, -1.0, -t),
Vector3::new(0.0, 1.0, -t),
Vector3::new(t, 0.0, -1.0),
Vector3::new(t, 0.0, 1.0),
Vector3::new(-t, 0.0, -1.0),
Vector3::new(-t, 0.0, 1.0),
],
cells: vec![
Triangle::new(0, 11, 5),
Triangle::new(0, 5, 1),
Triangle::new(0, 1, 7),
Triangle::new(0, 7, 10),
Triangle::new(0, 10, 11),
Triangle::new(1, 5, 9),
Triangle::new(5, 11, 4),
Triangle::new(11, 10, 2),
Triangle::new(10, 7, 6),
Triangle::new(7, 1, 8),
Triangle::new(3, 9, 4),
Triangle::new(3, 4, 2),
Triangle::new(3, 2, 6),
Triangle::new(3, 6, 8),
Triangle::new(3, 8, 9),
Triangle::new(4, 9, 5),
Triangle::new(2, 4, 11),
Triangle::new(6, 2, 10),
Triangle::new(8, 6, 7),
Triangle::new(9, 8, 1),
],
}
}
}
JSON Serialization
To prove this works, we need to be able to output our shape to some format that will be able to be rendered. Coming from a JS background, I’m only familiar with rendering shapes with WebGL. So, I need to be able to serialize the shape to JSON so I can load it in JS.
There’s an amazing library in Rust called
serde that will make this very
straightforward. We just need to import it and impl Serialize for all of our
structs.
The JSON structure we want will look like this. This is what Three.js expects
when initializing
BufferGeometry.
{
"positions": [
[
-0.8506508,
0,
0.5257311
],
...
],
"cells": [
[
0,
1,
2,
],
...
],
}
For the "cells" array, we’ll need to serialize Triangle into an array of 3
integer arrays:
impl Serialize for Triangle {
fn serialize<S>(&self, serializer: S) -> Result<S::Ok, S::Error>
where
S: Serializer,
{
let vec_indices = vec![self.a, self.b, self.c];
let mut seq = serializer.serialize_seq(Some(vec_indices.len()))?;
for index in vec_indices {
seq.serialize_element(&index)?;
}
seq.end()
}
}
I had some trouble serializing the cgmath::Vector3 to an array, so I made my
own type that wrapped Vector3 that could be serialized to an array of 3
floats.
#[derive(Debug)]
pub struct ArraySerializedVector(pub Vector3<f32>);
impl Serialize for ArraySerializedVector {
fn serialize<S>(&self, serializer: S) -> Result<S::Ok, S::Error>
where
S: Serializer,
{
let values = vec![self.0.x, self.0.y, self.0.z];
let mut seq = serializer.serialize_seq(Some(values.len()))?;
for value in values {
seq.serialize_element(&value)?;
}
seq.end()
}
}
And now Polyhedron needs to use this new type and implement Serialize for
the whole shape to get serialized:
#[derive(Serialize, Debug)]
pub struct Polyhedron {
pub positions: Vec<ArraySerializedVector>,
pub cells: Vec<Triangle>,
}
The actual serialization is done with:
fn write_to_json_file(polyhedron: Polyhedron, path: &Path) {
let mut json_file = File::create(path).expect("Can't create file");
let json = serde_json::to_string(&polyhedron).expect("Problem serializing");
json_file
.write_all(json.as_bytes())
.expect("Can't write to file");
}
On the JS side, the .json file can be read and simply fed into either Three.js
or regl to be rendered in WebGL (more on
that later).

Subdivided Icosahedron
Now, we need to take our regular icosahedron and subdivide its faces N number of times to generate an icosahedron with a detail level of N.
I pretty much copied must of the subdividing code from Three.js directly into Rust.
I won’t bore you with the details here, you can find the function here.

Truncated Icosahedron
Now we get to the meat of this project. Transforming an icosahedron into a hexsphere by truncating the points of the icosahedron into hexagon and pentagon faces.
You can imagine this operation as literally cutting off the points of the subdivided icosahedron at exactly the midpoint between the point and it’s six or five neighboring points.
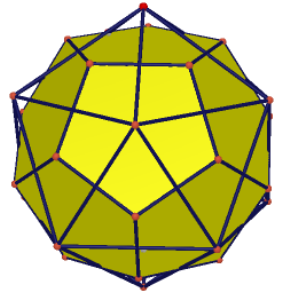
In this image you can see the regular icosahedron (0 subdivisions) in wireframe with a yellow shape underneath which is the result of all 12 points truncated to 12 pentagon faces, in other words: the regular dodecahedron.
You can see that the points of the new pentagon faces will be the exact center of the original triangular faces. It should now make sense why truncating a shape with 20 faces of 3 edges each results in a shape with 12 faces of 5 edges each. Each pair multiplied still equals 60.
Algorithm
There are many different algorithms you could use to generate the truncated shape, but this is roughly what I came up with:
-
Store a map of every icosahedron vertex to faces composed from that vertex (
vert_to_faces). -
Calculate and cache the centroid of every triangle in the icosahedron (
triangle_centroids). -
For every vertex in the original icosahedron:
-
Find the center point between all of centroids of all of the faces for that vertex (
center_point). This is essentially the original icosahedron point but lowered towards the center of the polygon since it will eventually be the center of a new flat hexagon face.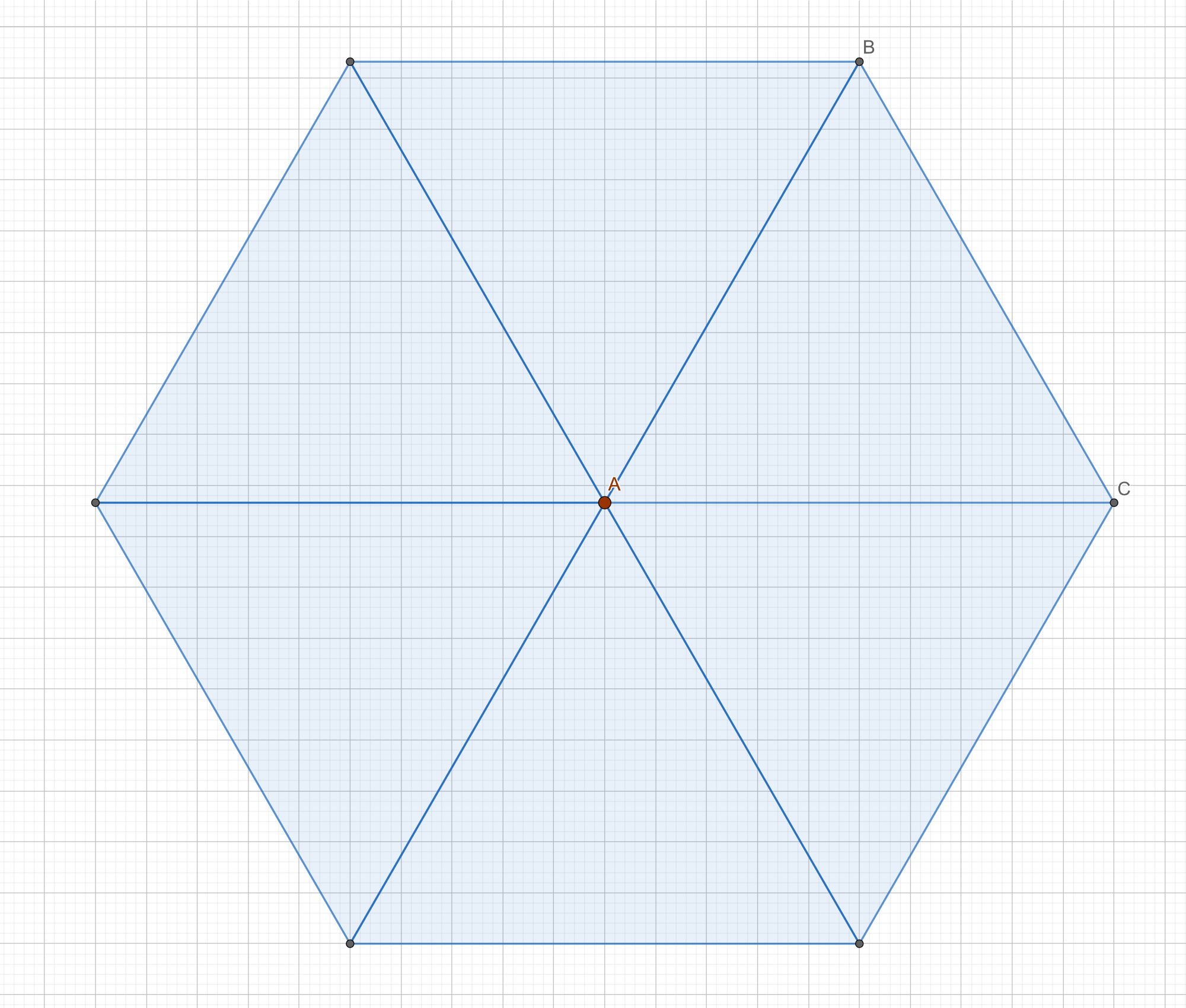
-
For every triangle face composed from the original vertex:
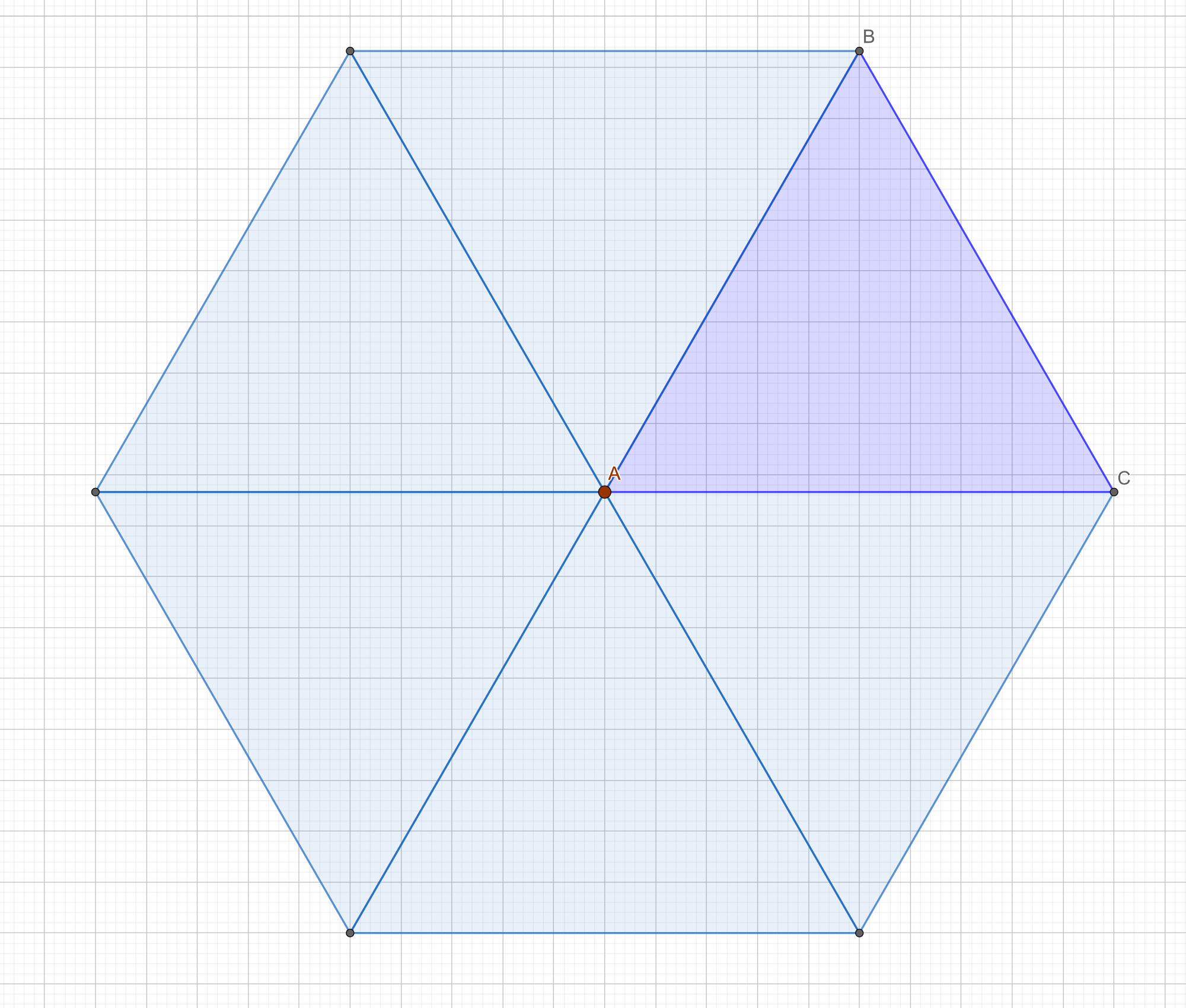
-
Sort the vertices of the triangle face so there is a vertex
Ain the center of the fan like in the image, and two other verticesBandCat the edges of the hexagon. -
Find the centroid of the selected face. This will be one of the five or six points of the new pentagon or hexagon (in brown in diagram below:
triangleCentroid). -
Find the mid point between
ABandAC(pointsmidABandmidACin diagram). -
With these mid points and the face centroid, we now have two new triangles (in orange below) that form one-fifth or one-sixth of the final pentagon or hexagon face. Add the points of the triangle to the
positionsarray. Add the two new triangles composed from those vertices as indexes into thepositionsarray to thecellsarray. We need to compose the pentagon or hexagon out of triangles because in graphics everything is a triangle, and this is the simplest way to tile either shape with triangles: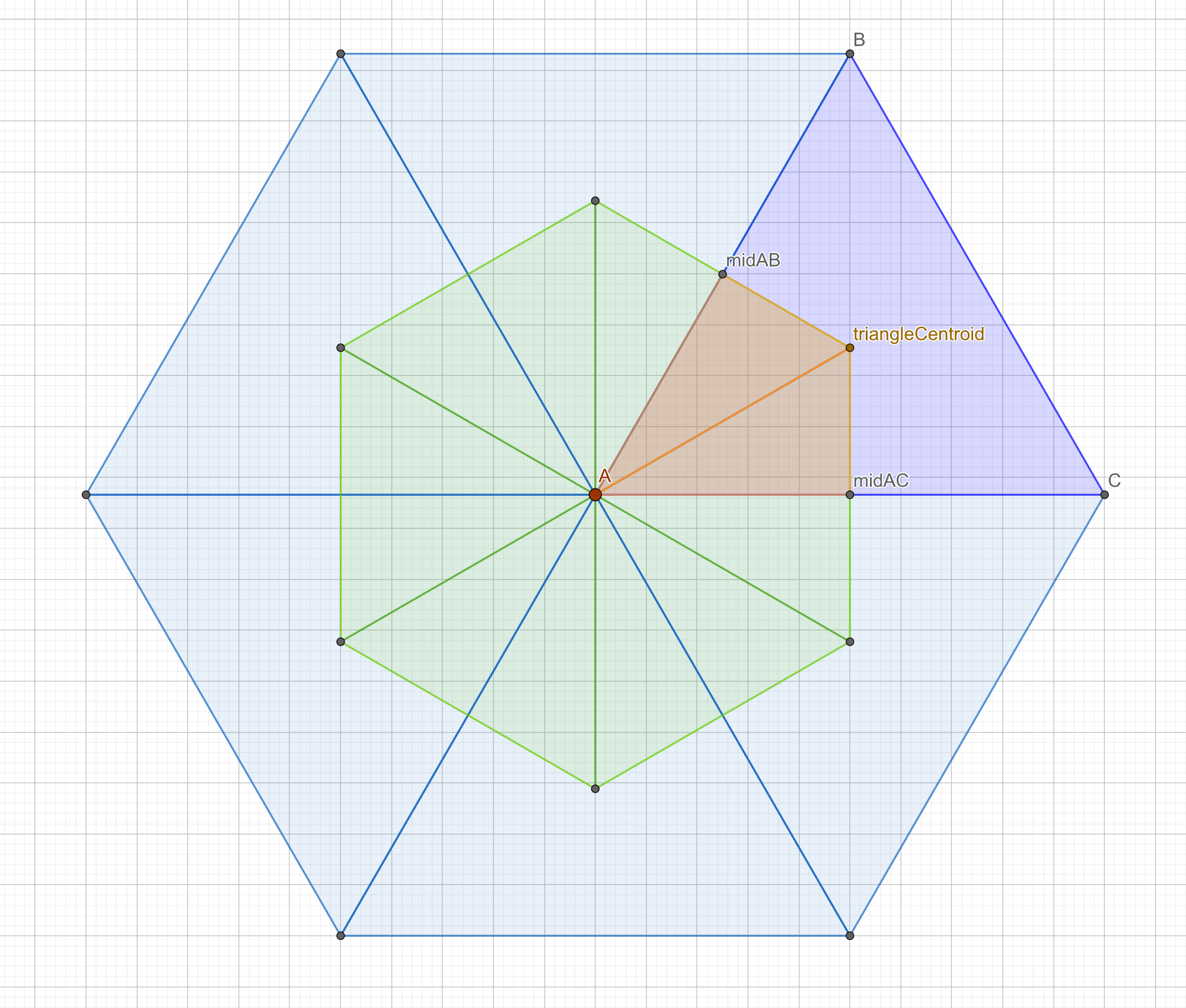
-
Go to step 5 until all faces of the icosahedron vertex have been visited.
Save indices to all new triangles in thecellsarray, which now form a complete pentagon or hexagon face, to thefacesarray.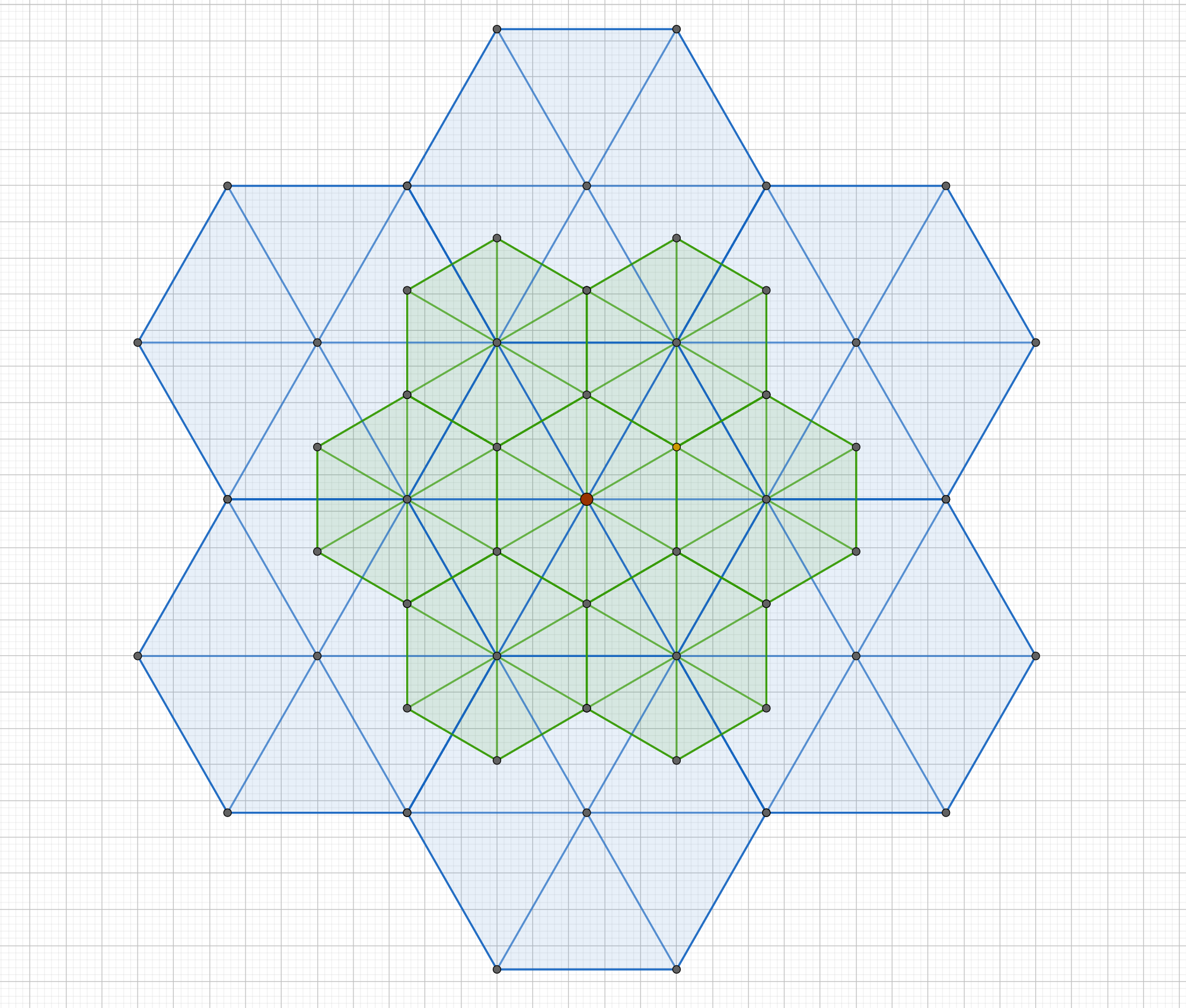
-
Go to step 3 until all vertices in the icosahedron have been visited. The truncated icosahedron is now complete.

Code
The truncate function calls out to a bunch of other functions, so here’s a
link to the function within the context of the whole
file.
Calculating Normals
It took me a surprisingly long time to figure out how to compute normals for the truncated icosahedron. I tried just using an out-of-the-box solution like angle-normals which could supposedly calculate the normal vectors for you, but they came out all wrong.

So, I tried doing it myself. Most tutorials on computing normal vectors for a mesh assume that it is tiled in a particular way. But, my algorithm spins around icosahedron points in all different directions, and so the triangle points are not uniformly in clockwise or counter-clockwise order.
I could have sorted these points into the correct order, but I found it easier to instead just detect when the normal was pointing the wrong way and just invert it.
pub fn compute_triangle_normals(&mut self) {
let origin = Vector3::new(0.0, 0.0, 0.0);
for i in 0..self.cells.len() {
let vertex_a = &self.positions[self.cells[i].a].0;
let vertex_b = &self.positions[self.cells[i].b].0;
let vertex_c = &self.positions[self.cells[i].c].0;
let e1 = vertex_a - vertex_b;
let e2 = vertex_c - vertex_b;
let mut no = e1.cross(e2);
// detect and correct inverted normal
let dist = vertex_b - origin;
if no.dot(dist) < 0.0 {
no *= -1.0;
}
let normal_a = self.normals[self.cells[i].a].0 + no;
let normal_b = self.normals[self.cells[i].b].0 + no;
let normal_c = self.normals[self.cells[i].c].0 + no;
self.normals[self.cells[i].a] = ArraySerializedVector(normal_a);
self.normals[self.cells[i].b] = ArraySerializedVector(normal_b);
self.normals[self.cells[i].c] = ArraySerializedVector(normal_c);
}
for normal in self.normals.iter_mut() {
*normal = ArraySerializedVector(normal.0.normalize());
}
}
Assigning Random Face Colors
Finally, all that’s left to generate is the face colors. The only way I could figure out how to individually color a shape’s faces in WebGL was to pass a color per vertex. The issue with this is that each vertex of the generated shapes could be shared between many different faces.
How can we solve this? At the cost of memory, we can just duplicate a vertex every time it’s used by a different triangle. That way no vertex is shared.
This can be done after a shape has been generated with shared vertices.
pub fn unique_vertices(&mut self, other: Polyhedron) {
for triangle in other.cells {
let vertex_a = other.positions[triangle.a].0;
let vertex_b = other.positions[triangle.b].0;
let vertex_c = other.positions[triangle.c].0;
let normal_a = other.normals[triangle.a].0;
let normal_b = other.normals[triangle.b].0;
let normal_c = other.normals[triangle.c].0;
self.positions.push(ArraySerializedVector(vertex_a));
self.positions.push(ArraySerializedVector(vertex_b));
self.positions.push(ArraySerializedVector(vertex_c));
self.normals.push(ArraySerializedVector(normal_a));
self.normals.push(ArraySerializedVector(normal_b));
self.normals.push(ArraySerializedVector(normal_c));
self.colors
.push(ArraySerializedVector(Vector3::new(1.0, 1.0, 1.0)));
self.colors
.push(ArraySerializedVector(Vector3::new(1.0, 1.0, 1.0)));
self.colors
.push(ArraySerializedVector(Vector3::new(1.0, 1.0, 1.0)));
let added_index = self.positions.len() - 1;
self.cells
.push(Triangle::new(added_index - 2, added_index - 1, added_index));
}
self.faces = other.faces;
}
With unique vertices, we can now generate a random color per face with the rand crate.
pub fn assign_random_face_colors(&mut self) {
let mut rng = rand::thread_rng();
for i in 0..self.faces.len() {
let face_color = Vector3::new(rng.gen(), rng.gen(), rng.gen());
for c in 0..self.faces[i].len() {
let face_cell = &self.cells[self.faces[i][c]];
self.colors[face_cell.a] = ArraySerializedVector(face_color);
self.colors[face_cell.b] = ArraySerializedVector(face_color);
self.colors[face_cell.c] = ArraySerializedVector(face_color);
}
}
}
Binary Serialization
Now that we have to duplicate vertices for individual face colors, the size of our JSON outputs are getting quite big:
| File | Size |
|---|---|
| icosahedron_r1_d6.json | 28 MB |
| icosahedron_r1_d7.json | 113 MB |
| hexsphere_r1_d5.json | 42 MB |
| hexsphere_r1_d6.json | 169 MB |
Since all of our data is just floating point numbers, we could reduce the size of the output considerably by using a binary format instead.
I used the byteorder crate to
write out all of the Vecs in my Polyhedron struct to a binary file in
little-endian order.
The binary format is laid out as:
- 1 32 bit unsigned integer specifying the number of vertices (
V) - 1 32 bit unsigned integer specifying the number of triangles (
T) V* 3 number of 32 bit floats for every vertex’s x, y, and z coordinateV* 3 number of 32 bit floats for the normals of every vertexV* 3 number of 32 bit floats for the color of every vertexT* 3 number of 32 bit unsigned integers for the 3 indices into the vertex array that make every triangle
The write_to_binary_file function which does all that is
here.
That’s a lot better:
| File | Size |
|---|---|
| icosahedron_r1_d6.bin | 9.8 MB |
| icosahedron_r1_d7.bin | 11 MB |
| hexsphere_r1_d5.bin | 14 MB |
| hexsphere_r1_d6.bin | 58 MB |
On the JavaScript side, the binary files can be read into Float32Arrays like
this:
fetch(binaryFile)
.then(response => response.arrayBuffer())
.then(buffer => {
let reader = new DataView(buffer);
let numVertices = reader.getUint32(0, true);
let numCells = reader.getUint32(4, true);
let shape = {
positions: new Float32Array(buffer, 8, numVertices * 3),
normals: new Float32Array(buffer, numVertices * 12 + 8, numVertices * 3),
colors: new Float32Array(buffer, numVertices * 24 + 8, numVertices * 3),
cells: new Uint32Array(buffer, numVertices * 36 + 8, numCells * 3),
})
Rendering in WebGL with Regl
I was initially rendering the shapes with Three.js but switched to regl because it seemed like a more direct abstraction over WebGL. It makes setting up a WebGL renderer incredibly easy compared to all of the dozens cryptic function calls you’d have to otherwise use.
This is pretty much all of the rendering code using regl in my 3D hexsphere and icosahedron viewer project.
const drawShape = hexsphere => regl({
vert: `
precision mediump float;
uniform mat4 projection, view;
attribute vec3 position, normal, color;
varying vec3 fragNormal, fragPosition, fragColor;
void main() {
fragNormal = normal;
fragPosition = position;
fragColor = color;
gl_Position = projection * view * vec4(position, 1.0);
}`,
frag: `
precision mediump float;
struct Light {
vec3 color;
vec3 position;
};
uniform Light lights[1];
varying vec3 fragNormal, fragPosition, fragColor;
void main() {
vec3 normal = normalize(fragNormal);
vec3 light = vec3(0.1, 0.1, 0.1);
for (int i = 0; i < 1; i++) {
vec3 lightDir = normalize(lights[i].position - fragPosition);
float diffuse = max(0.0, dot(lightDir, normal));
light += diffuse * lights[i].color;
}
gl_FragColor = vec4(fragColor * light, 1.0);
}`,
attributes: {
position: hexsphere.positions,
normal: hexsphere.normals,
color: hexsphere.colors,
},
elements: hexsphere.cells,
uniforms: {
"lights[0].color": [1, 1, 1],
"lights[0].position": ({ tick }) => {
const t = 0.008 * tick
return [
1000 * Math.cos(t),
1000 * Math.sin(t),
1000 * Math.sin(t)
]
},
},
})
I also imported regl-camera which handled all of the complex viewport code for me.
It was fairly easy to get a simple renderer working quickly in regl, but I couldn’t find many examples of more complex projects using regl. Unfortunately, the project looks a bit unmaintained these days as well. If I’m going to continue with rendering in WebGL, I think I will try out Babylon.js instead.
Running in WebAssembly
Since rust can be compiled down to wasm and then run in the browser, I briefly tried getting the project to run completely in the browser.
The wasm-pack tool made it pretty easy to get started. My main struggle was figuring out an efficient way to get the megabytes of generated shape data into the JavaScript context so it could be rendered in WebGL.
The best I could come up with was to export all of my structs into flat
Vec<f32>s and then create Float32Arrays from the JS side that are views into
wasm’s memory.
To export:
pub fn fill_exports(&mut self) {
for position in &self.positions {
self.export_positions.push(position.0.x);
self.export_positions.push(position.0.y);
self.export_positions.push(position.0.z);
}
for normal in &self.normals {
self.export_normals.push(normal.0.x);
self.export_normals.push(normal.0.y);
self.export_normals.push(normal.0.z);
}
for color in &self.colors {
self.export_colors.push(color.0.x);
self.export_colors.push(color.0.y);
self.export_colors.push(color.0.z);
}
for cell in &self.cells {
self.export_cells.push(cell.a as u32);
self.export_cells.push(cell.b as u32);
self.export_cells.push(cell.c as u32);
}
}
And then the wasm lib.rs:
use byteorder::{LittleEndian, WriteBytesExt};
use js_sys::{Array, Float32Array, Uint32Array};
use wasm_bindgen::prelude::*;
use web_sys::console;
mod icosahedron;
#[cfg(feature = "wee_alloc")]
#[global_allocator]
static ALLOC: wee_alloc::WeeAlloc = wee_alloc::WeeAlloc::INIT;
#[wasm_bindgen(start)]
pub fn main_js() -> Result<(), JsValue> {
#[cfg(debug_assertions)]
console_error_panic_hook::set_once();
Ok(())
}
#[wasm_bindgen]
pub struct Hexsphere {
positions: Float32Array,
normals: Float32Array,
colors: Float32Array,
cells: Uint32Array,
}
#[wasm_bindgen]
pub fn shape_data() -> Result<Array, JsValue> {
let radius = 1.0;
let detail = 7;
let mut hexsphere = icosahedron::Polyhedron::new_truncated_isocahedron(radius, detail);
hexsphere.compute_triangle_normals();
let mut unique_hexsphere = icosahedron::Polyhedron::new();
unique_hexsphere.unique_vertices(hexsphere);
unique_hexsphere.assign_random_face_colors();
unique_hexsphere.fill_exports();
let positions = unsafe { Float32Array::view(&unique_hexsphere.export_positions) };
let normals = unsafe { Float32Array::view(&unique_hexsphere.export_normals) };
let colors = unsafe { Float32Array::view(&unique_hexsphere.export_colors) };
let cells = unsafe { Uint32Array::view(&unique_hexsphere.export_cells) };
Ok(Array::of4(&positions, &normals, &colors, &cells))
}
With wasm-pack, I could import the wasm package, run the shape_data()
function, and then read the contents as any other normal JS array.
let rust = import("../pkg/index.js")
rust.then(module => {
const shapeData = module.shape_data()
const shape = {
positions: shapeData[0],
normals: shapeData[1],
colors: shapeData[2],
cells: shapeData[3],
}
...
})
I could side-step the issue of transferring data from Rust to JavaScript entirely by programming literally everything in WebAssembly. But the bindings from rust wasm to the WebGL API are still way too complicated compared to just using regl. Plus, I’d have to implement my own camera from scratch.
The Stats
So how much faster is Rust than JavaScript in generating icosahedrons and hexspheres?
Here’s how long it took with generating shapes in JS with Three.js in Firefox versus in native Rust with a i5-2500K 3.3 GHz CPU.
| Shape | JS generate time | Rust generate time |
|---|---|---|
| Icosahedron detail 6 | 768 ms | 28.23 ms |
| Icosahedron detail 7 | 4.25 s | 128.81 ms |
| Hexsphere detail 6 | 11.37 s | 403.10 ms |
| Hexsphere detail 7 | 25.49 s | 1.85 s |
So much faster!
Todo
-
Add a process that alters the shape post-generation. Part of the reason why I decided to fan the hexagon faces with so many triangles is that it also allows me to control the height of the faces better. This could eventually allow me to create mountain ranges and river valleys on a hexsphere planet. Stretching and pulling the edges of the polygon faces in random directions could add variation and make for a more organic looking hexsphere.
-
Conversely, it would be nice to be able to run a process post-generation that could reduce the number of triangles by tiling the hexagons more efficiently when face elevation isn’t needed.
-
Add parameters to the generation that allows generating sections of the hexsphere / icosahedron. This will be essential for rendering very detailed polyhedrons since at a certain detail level it becomes impossible to render the entire shape at once.
In WebGL, figure out what part of the shape is in the current viewport and pass these parameters to the generation.
-
Render the shapes in a native Rust graphics library instead of WebGL. I’m curious how much slower WebGL is making things.
-
Parallelize the generation. Right now the generation is very CPU bound and each subdivide/truncate iteration is mostly independent from each other, so I think I could get some decent speed-up by allowing the process to run on multiple cores. Perhaps the rayon crate could make this pretty straightforward.
-
Find some way to avoid unique vertices. The size of the shape is much bigger because of this. There might be a way to keep shared vertices while also having a separate color per face by using texture mapping.
-
In the renderer, implement face selection (point and click face and show an outline around selected face).
-
In the renderer, implement fly-to-face zooming: given a face, fly the camera around the sphere in an orbit and then zoom in on the face.
 (
(